Sensitivity Analysis of an Ordinary Differential Equation (ODE)

MADS is applied to perform sensitivity analysis of an Ordinary Differential Equation (ODE).

The analyses below are performed using examples/ode/ode.jl.

ODE

Analyzed ODE looks like this:

\[x''(t) = -\omega^2 * x(t) - k * x'(t)\]

Unknown ODE parameters:

• k

• \[\omega\]

Example ODE solution:

For model parameters:

• k = 0.1

• \[\omega\]

  = 0.2

Local sensitivity analysis

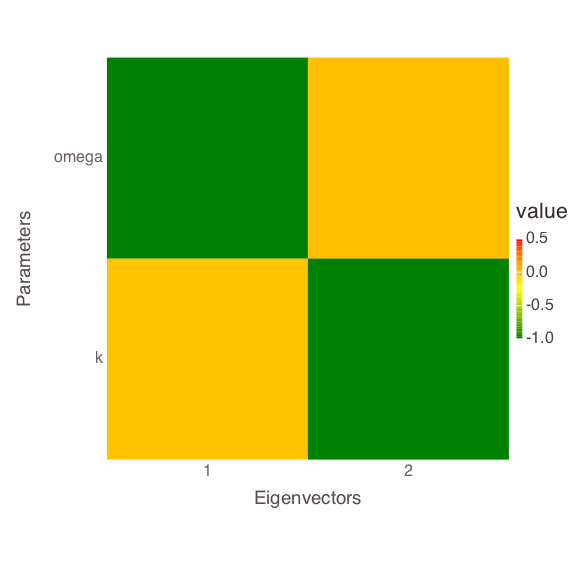
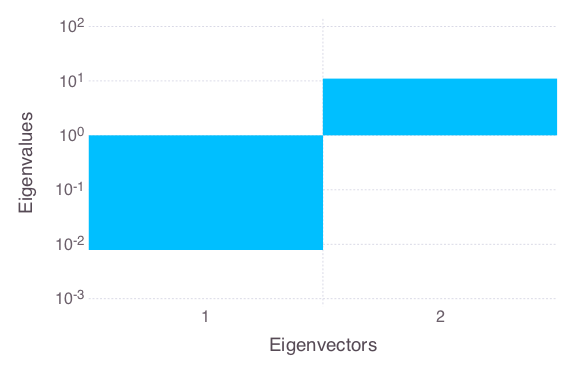
Global sensitivity analysis (using eFAST)

Probabilistic distributions of the prior parameter uncertainties are:

• k = LogUniform(0.01, 0.1)

• \[\omega\]

  = Uniform(0.1, 0.3)

Bayesian sensitivity analysis

Observations

Synthetic observations are applied to constrain the ODE parameters:

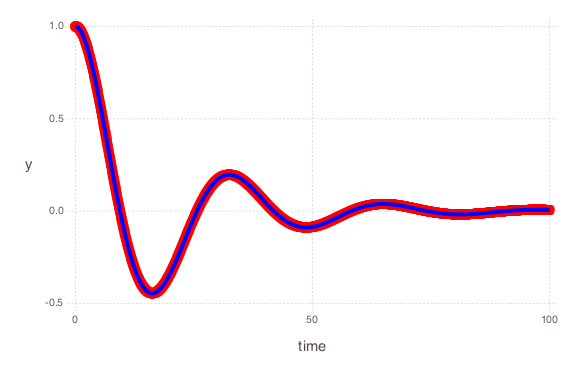
Observation errors are equal for all the sample locations with standard deviation equal to 1 (observation weight = 1 / observation standard deviation = 1 / 1 = 1)

Prior parameter uncertainties

k only

$\omega$ only

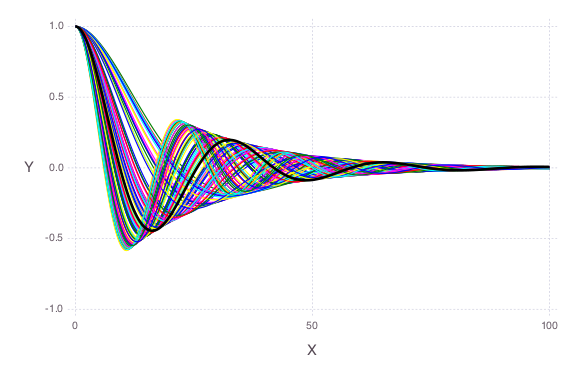
Both parameters

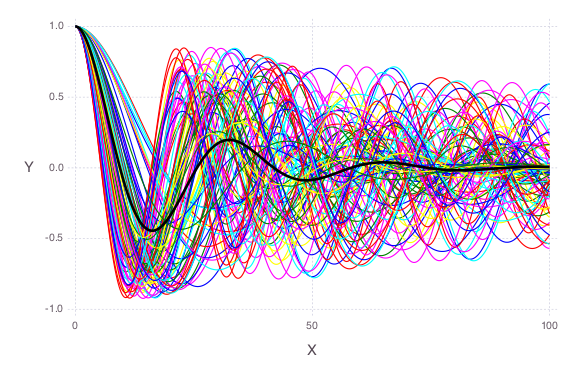
The observation data are plotted as a solid black line.

Histograms/scatter plots of Bayesian MCMC results

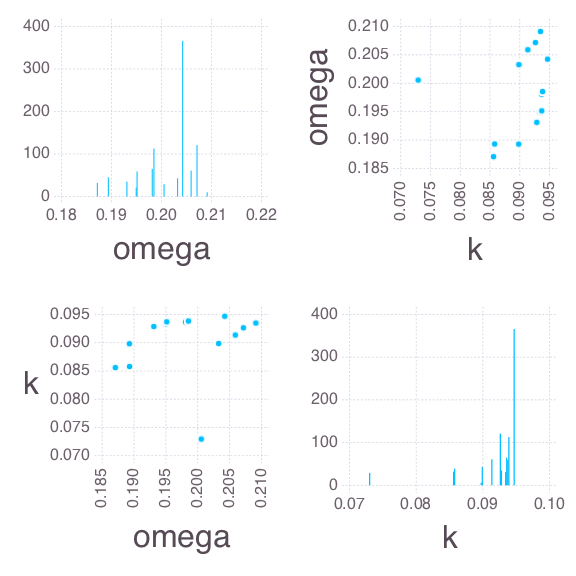
Posterior parameter uncertainties

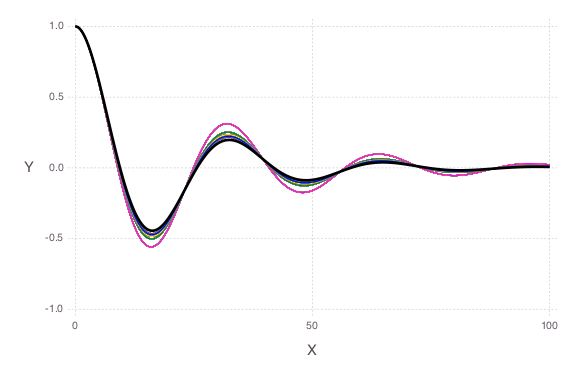
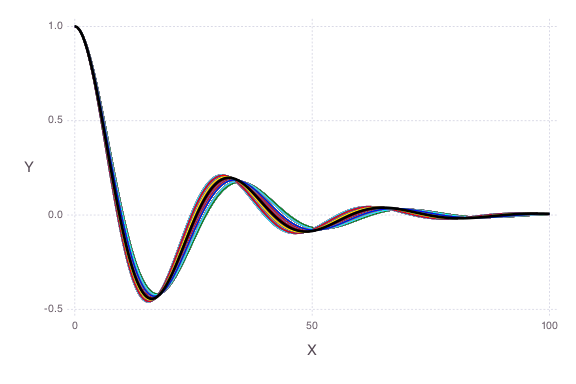
Note that now the parameter uncertainties are constrained by the observation data.

k only

$\omega$ only

Both parameters

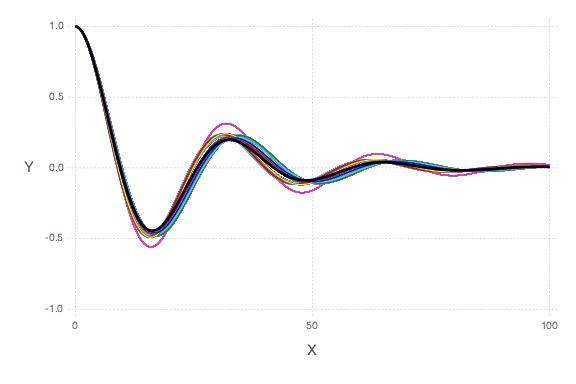
The observation data are plotted as a solid black line.