Information Gap Decision Analysis

MADS is applied to execute Information Gap Decision Analysis.

The analyses below are performed using examples/model_analysis/infogap.jl.

Setup

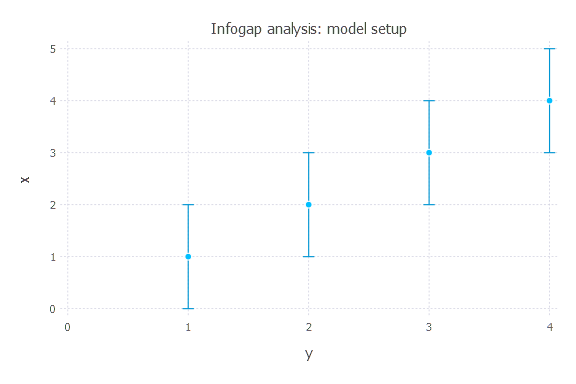
• There are 4 uncertain observations at times t = [1, 2, 3, 4]

• There are 4 possible models that can be applied to match the data

  1. y(t) = a * t + c
  2. y(t) = a * t^(1.1) + b * t + c
  3. y(t) = a * t^n + b * t + c
  4. y(t) = a * exp(t * n) + b * t + c

• There are 4 unknown model parameters with uniform prior probability functions:

  1. a = Uniform(-10, 10)
  2. b = Uniform(-10, 10)
  3. c = Uniform(-5, 5)
  4. n = Uniform(-3, 3)

• The model prediction for t = 5 is unknown and information gap prediction uncertainty needs to be evaluated

• The horizon of information gap uncertainty h is applied to define the acceptable deviations in the 4 uncertain observations.

• Below we explore infogap of each model for different h values.

Infogap in Model 1

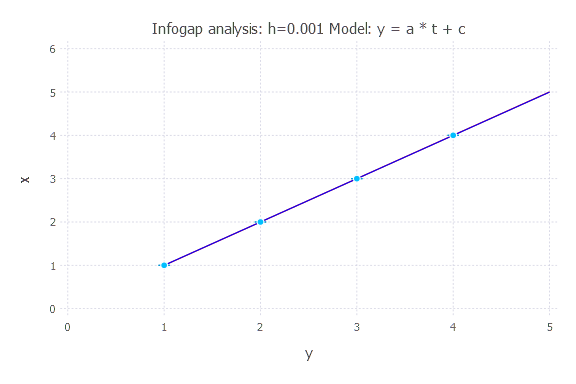
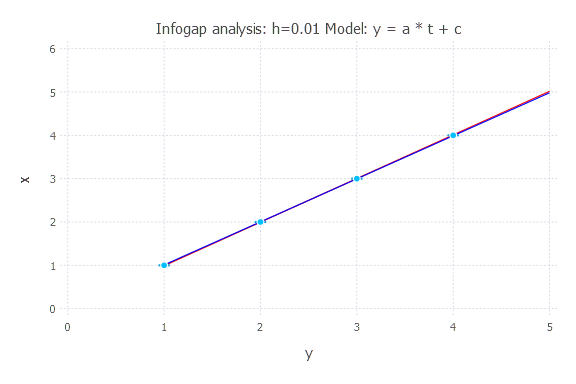
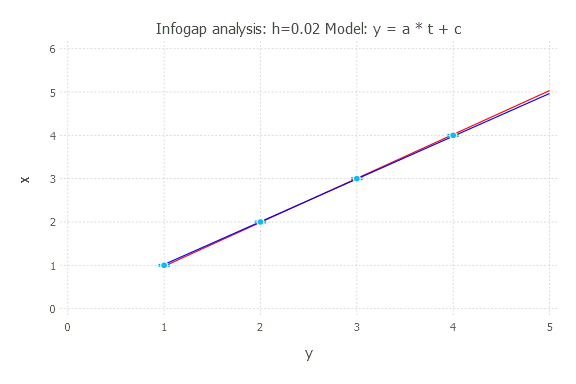
Model: y(t) = a * t + c

• h = 0.001

• h = 0.01

• h = 0.02

• h = 0.05

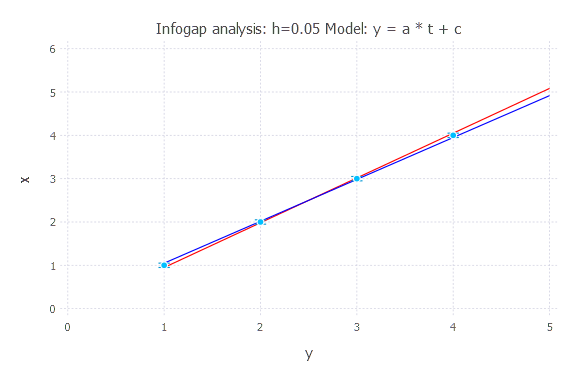
• h = 0.1

• h = 0.2

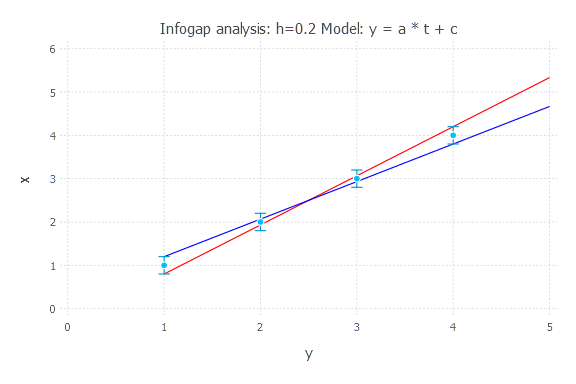
• h = 0.5

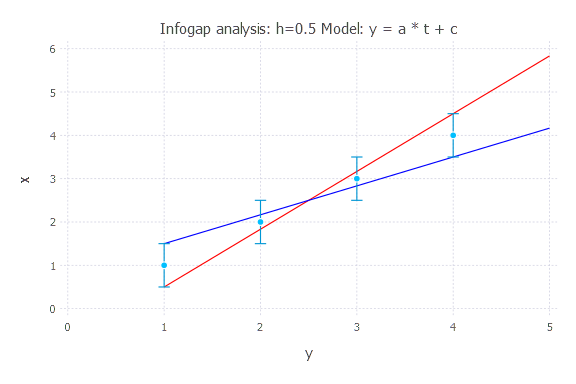
• h = 1.0

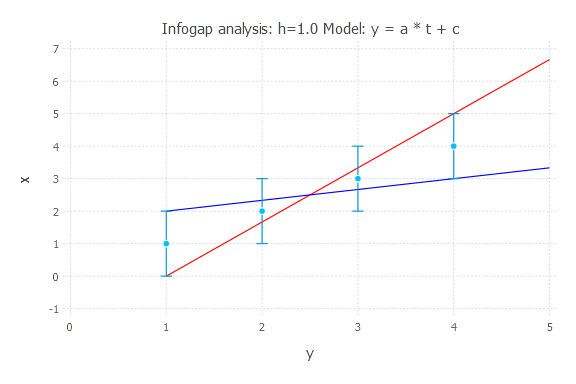
Infogap in Model 2

Model: y(t) = a * t^(1.1) + b * t + c

• h = 0.001

• h = 0.01

• h = 0.02

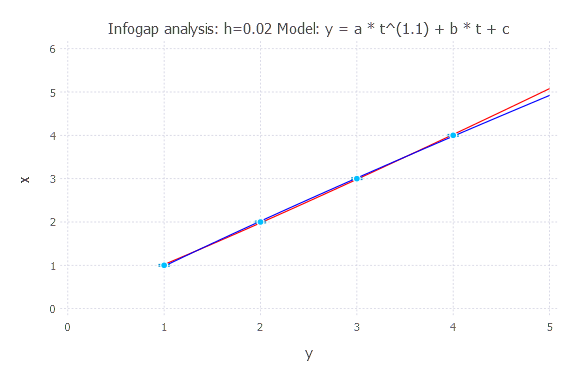
• h = 0.05

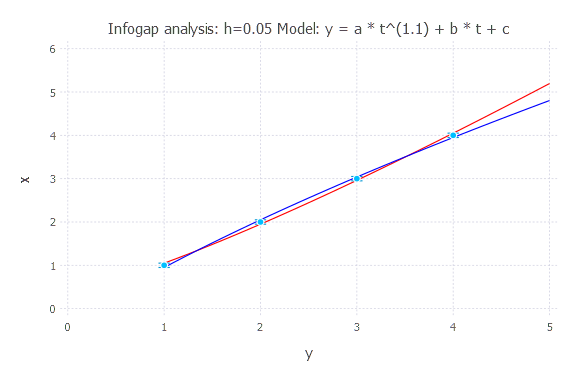
• h = 0.1

• h = 0.2

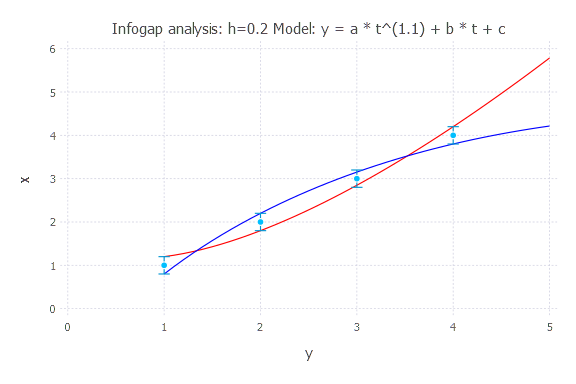
• h = 0.5

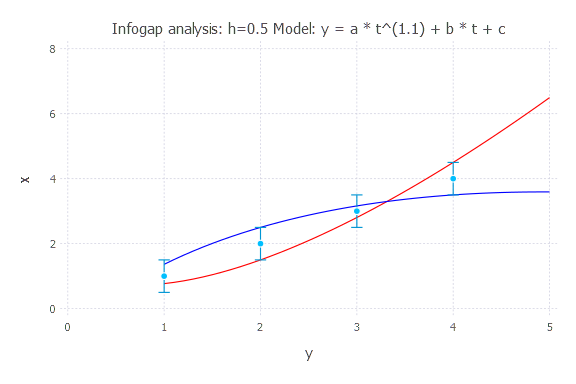
• h = 1.0

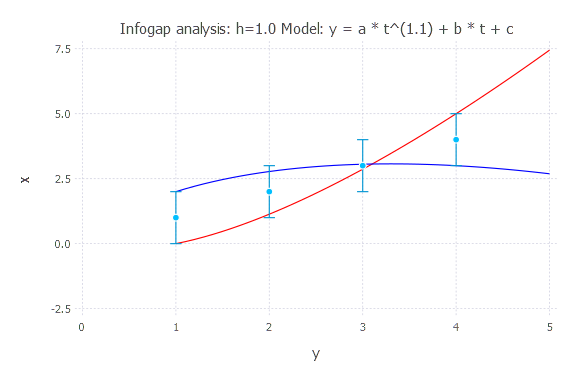
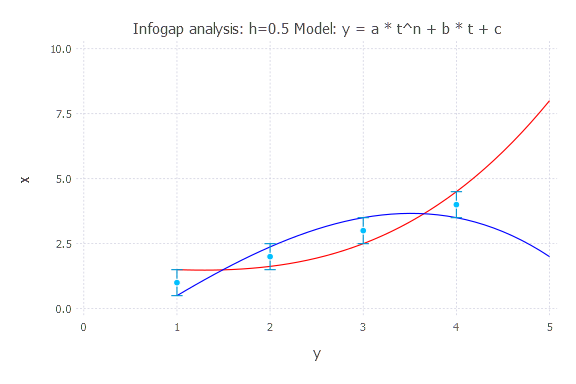
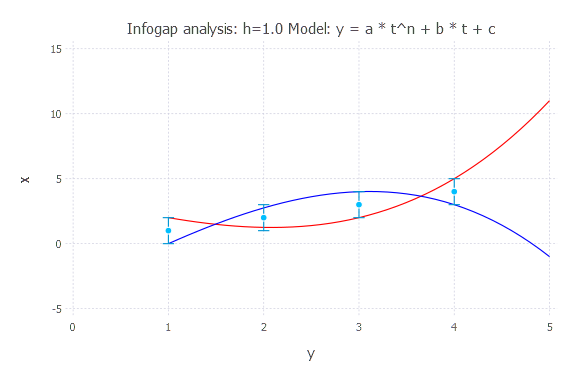
Infogap in Model 3

Model: y(t) = a * t^n + b * t + c

• h = 0.001

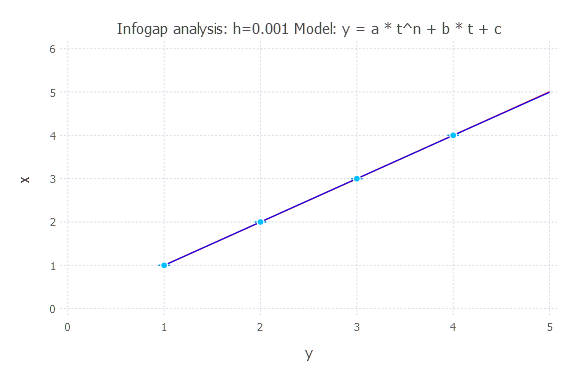
• h = 0.01

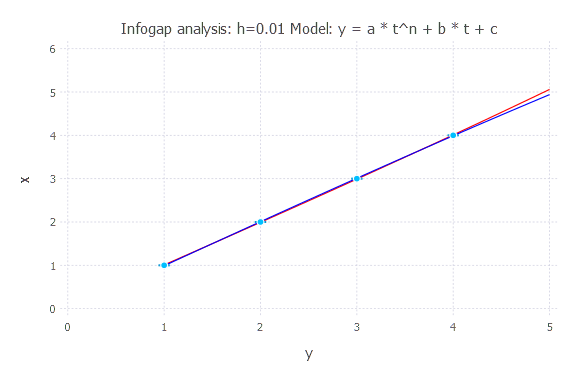
• h = 0.02

• h = 0.05

• h = 0.1

• h = 0.2

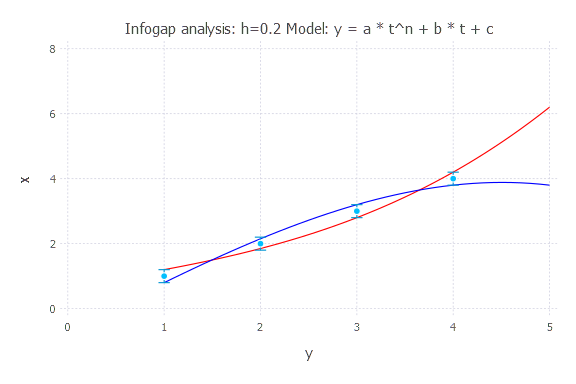
• h = 0.5

• h = 1.0

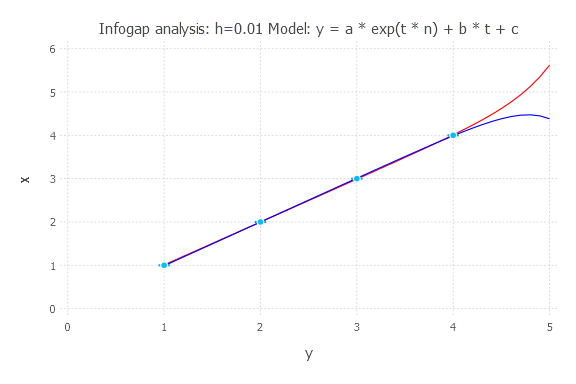
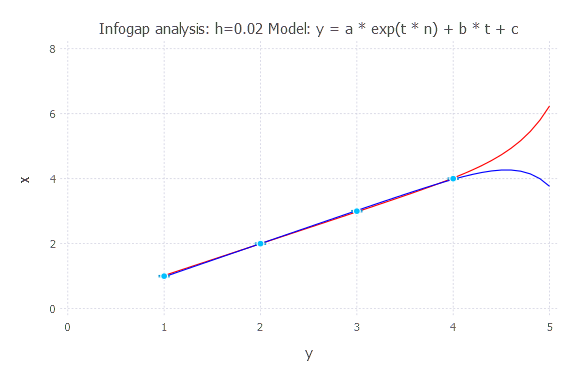
Infogap in Model 4

Model: y(t) = a * exp(t * n) + b * t + c

• h = 0.001

• h = 0.01

• h = 0.02

• h = 0.05

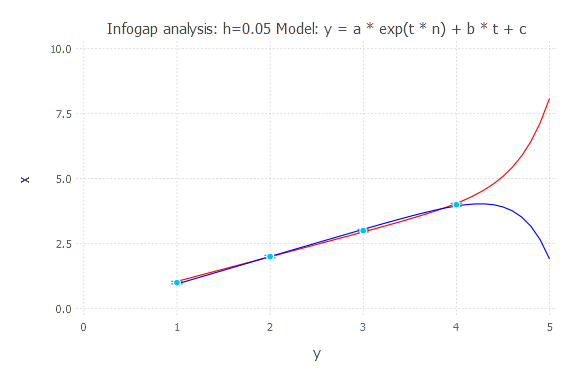
• h = 0.1

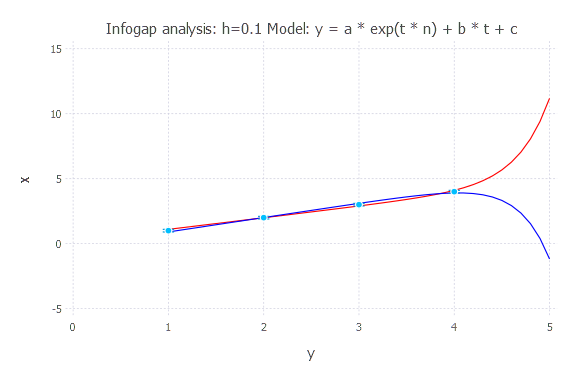
• h = 0.2

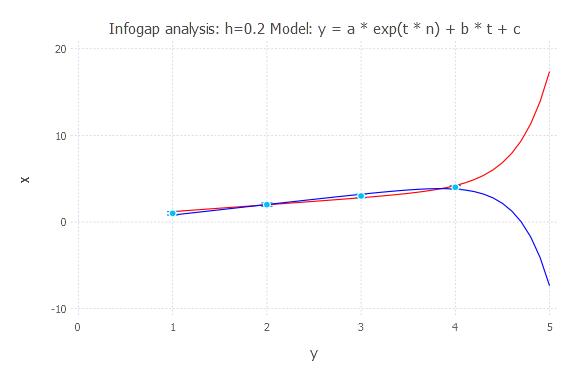
• h = 0.5

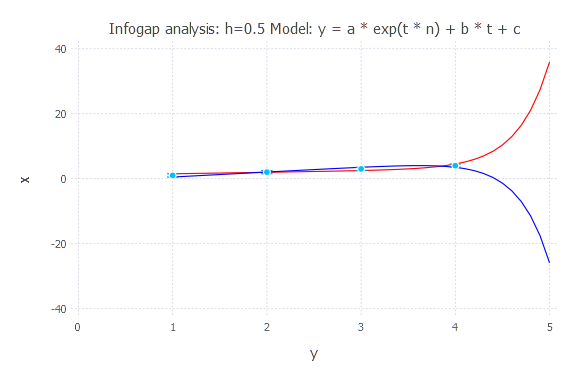
• h = 1.0

Opportuneness and Robustness

Based on the figures above, the last model (y(t) = a * exp(t * n) + b * t + c) is associated with the largest infogap uncertainties.

It has the lowest robustness and highest opportuneness.